
| decimal numbers: | ||
| exponential numbers: |
| acceleration of gravity: |
It is assumed that the gas can be considered to be an ideal gas and that the calorically perfect gas assumption applies.
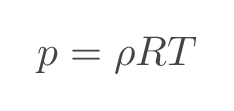
With the assumptions above, speed of sound is a function of temperature and gas properties
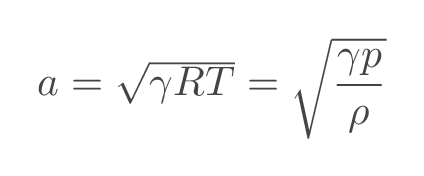
Specific heat at constant pressure, \(C_p\), and specific heat at constant temperature, \(C_v\), are calculated from the specified gas data according to:
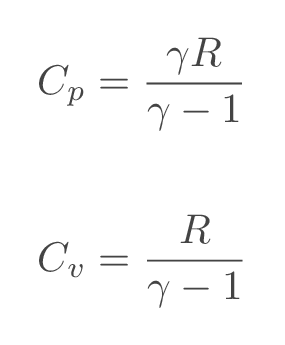
The sonic conditions (starred quantities) are the flow conditions that we would get if we could slow down or accelerate the fluid to sonic speed adiabatically (without adding or removing heat). If the sonic conditions are normalized suing the corresponding total/stagnation properties (the flow conditions we would get if we could slow the fluid down to zero velocity isentropically), it becomes a constant for a specific gas.
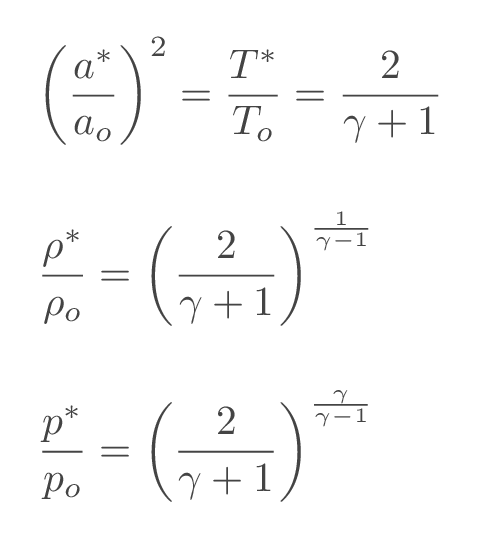
More details can be found here:
| Introduction to Fluid Mechanics - Basic Concepts | (Fluid properties) |
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
It is assumed that the gas can be considered to be an ideal gas and that the calorically perfect gas assumption applies.
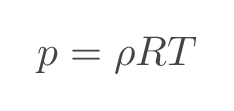
With the assumptions above, speed of sound is a function of temperature and gas properties
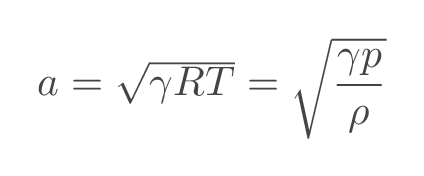
Specific heat at constant pressure, \(C_p\), and specific heat at constant temperature, \(C_v\), are calculated from the specified gas data according to:
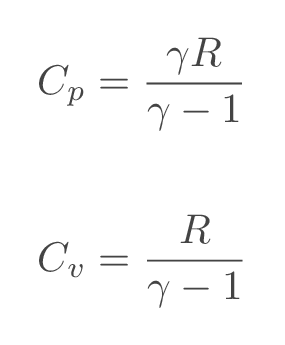
The sonic conditions (starred quantities) are the flow conditions that we would get if we could slow down or accelerate the fluid to sonic speed adiabatically (without adding or removing heat). If the sonic conditions are normalized suing the corresponding total/stagnation properties (the flow conditions we would get if we could slow the fluid down to zero velocity isentropically), it becomes a constant for a specific gas.
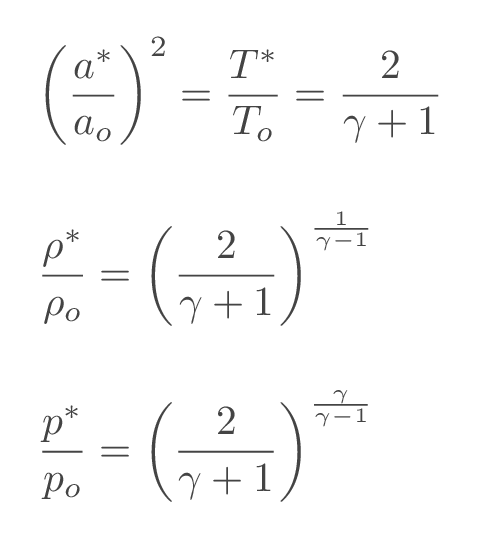
More details can be found here:
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
| Select problem type | ||||||
| vertical distance between plates \(\left(H\right)\): | ||||||
| lower wall velocity \(\left(V_1\right)\): | ||||||
| upper wall velocity \(\left(V_2\right)\): | ||||||
| pressure gradient \(\left(dp/dx\right)\): | ||||||
It is assumed that the gas can be considered to be an ideal gas and that the calorically perfect gas assumption applies.
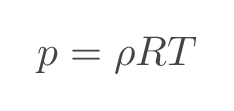
With the assumptions above, speed of sound is a function of temperature and gas properties
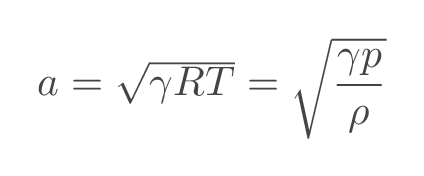
Specific heat at constant pressure, \(C_p\), and specific heat at constant temperature, \(C_v\), are calculated from the specified gas data according to:
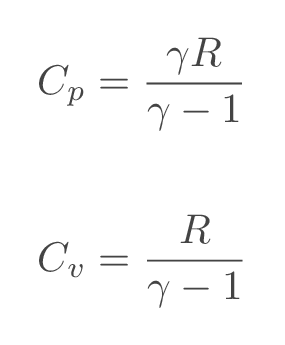
The sonic conditions (starred quantities) are the flow conditions that we would get if we could slow down or accelerate the fluid to sonic speed adiabatically (without adding or removing heat). If the sonic conditions are normalized suing the corresponding total/stagnation properties (the flow conditions we would get if we could slow the fluid down to zero velocity isentropically), it becomes a constant for a specific gas.
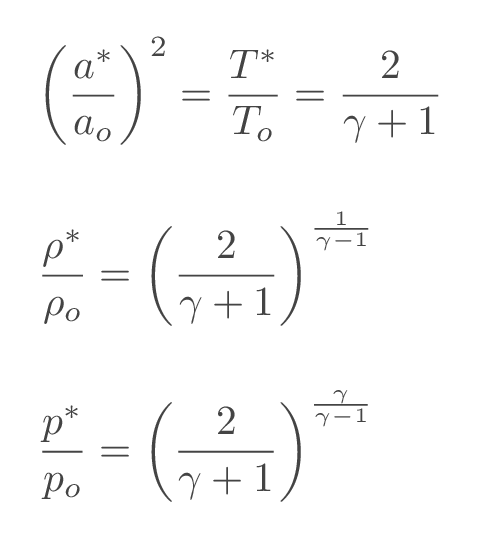
More details can be found here:
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
| Select problem type | |||||
| Reynolds number \(\left(Re_{D_{lam}}\right)\): | ||||||
| Reynolds number \(\left(Re_{D_{turb}}\right)\): |
| Reynolds number \(\left(Re_D\right)\): | ||||||
| average velocity \(\left(V\right)\): | ||||||
| volume flow \(\left(Q\right)\): | ||||||
| average velocity \(\left(u_{max}\right)\): | ||||||
| average velocity \(\left(dp/dx\right)\): | ||||||
| friction head \(\left(h_f\right)\): |
| pipe diameter \(\left(D\right)\): | ||||||
| pipe length \(\left(L\right)\): |
| relative roughness \(\left(\epsilon/D\right)\): | ||||||
| absolute roughness \(\left(\epsilon\right)\): |
It is assumed that the gas can be considered to be an ideal gas and that the calorically perfect gas assumption applies.
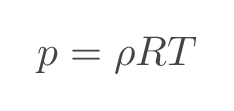
With the assumptions above, speed of sound is a function of temperature and gas properties
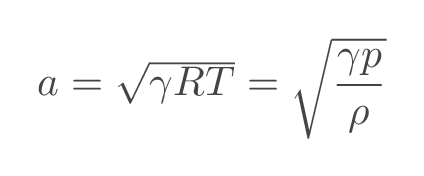
Specific heat at constant pressure, \(C_p\), and specific heat at constant temperature, \(C_v\), are calculated from the specified gas data according to:
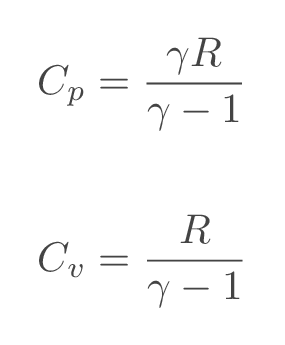
The sonic conditions (starred quantities) are the flow conditions that we would get if we could slow down or accelerate the fluid to sonic speed adiabatically (without adding or removing heat). If the sonic conditions are normalized suing the corresponding total/stagnation properties (the flow conditions we would get if we could slow the fluid down to zero velocity isentropically), it becomes a constant for a specific gas.
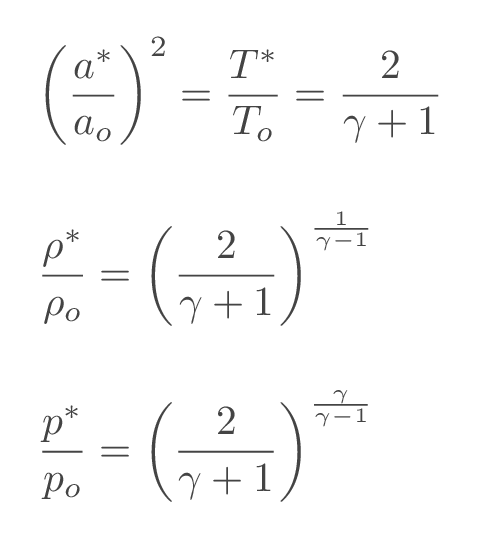
More details can be found here:
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
| Select problem type | ||||||
| Reynolds number \(\left(Re_x\right)\): | ||||||
| freestream velocity \(\left(U\right)\): | ||||||
| axial coordinate \(\left(x\right)\): | ||||||
| flat plate width \(\left(b\right)\): | ||||||
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
| Select problem type | ||||||
| Reynolds number \(\left(Re_x\right)\): | ||||||
| freestream velocity \(\left(U\right)\): | ||||||
| axial coordinate \(\left(x\right)\): | ||||||
| flat plate width \(\left(b\right)\): | ||||||
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
It is assumed that the gas can be considered to be an ideal gas and that the calorically perfect gas assumption applies.
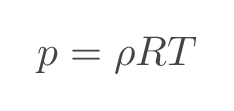
With the assumptions above, speed of sound is a function of temperature and gas properties
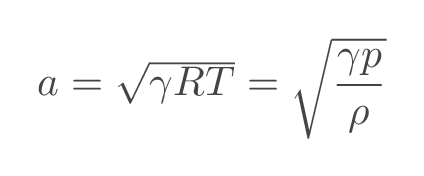
Specific heat at constant pressure, \(C_p\), and specific heat at constant temperature, \(C_v\), are calculated from the specified gas data according to:
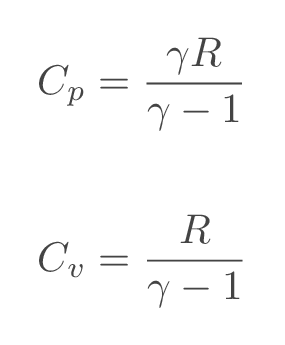
The sonic conditions (starred quantities) are the flow conditions that we would get if we could slow down or accelerate the fluid to sonic speed adiabatically (without adding or removing heat). If the sonic conditions are normalized suing the corresponding total/stagnation properties (the flow conditions we would get if we could slow the fluid down to zero velocity isentropically), it becomes a constant for a specific gas.
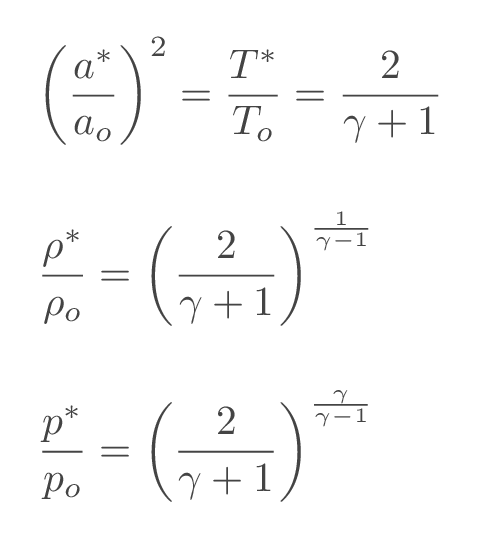
More details can be found here:
| Select problem type | |||||
| fluid density \(\left(\rho\right)\): | ||||
| fluid viscosity \(\left(\nu\right)\): |
| Reynolds number \(\left(Re_{D}\right)\): | ||||||
| freestream velocity \(\left(U\right)\): | ||||||
| diameter \(\left(D\right)\): |
