
HEAT is a JavaScript-based calculator for heat transfer problems. HEAT is under development and will appear in a future OFC release.
| decimal numbers: | ||
| exponential numbers: |
An expansion region or expansion fan is generated in a supersonic flow when the flow direction needs to change such that the flow area increases - the flow turns out from itself. The expansion region constitutes a collection of an infinite number of Mach waves. Each Mach wave contributes with an infinitesimal change in flow direction and flow properties without introduction of losses i.e., the process is isentropic. Thus, the integrated effect over the expansion region is also isentropic. In the figure below, the sharp expansion corner (left figure) will lead to the generation of a centered simple wave or expansion fan and the gradual expansion (right figure) will generate a simple wave (that might be centered depending on the shape of the wall)
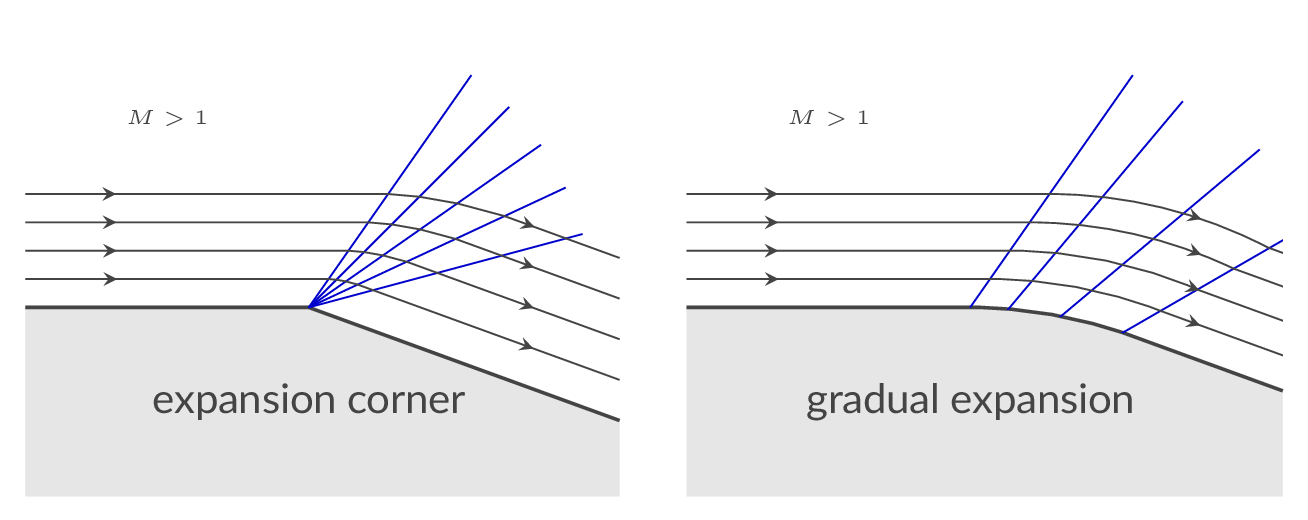
The expansion fan (Prandtl-Meyer expansion) generated at the expansion corner in the figure below will gradually change the flow direction and the end result is a net turning of the flow such that it follows the wall downstream of the corner.

The left and right ends of the expansion fan are defined by the angle of Mach waves in the upstream and downstream region, respectively.

The net turning may be calculated as follows:
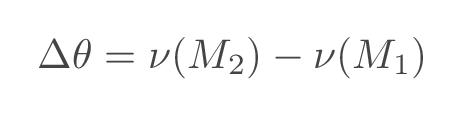
where \(\nu(M)\) is the Prandtl-Meyer function evaluated at a position with Mach number \(M\)
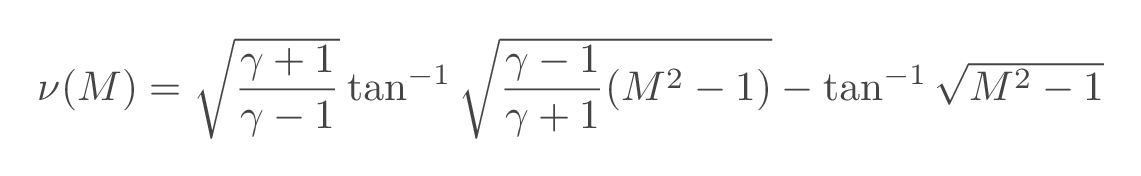
| flow property | change over expansion region |
|---|---|
| density | decreases |
| pressure | decreases |
| temperature | decreases |
| velocity | increases |
| Mach number | increases |
More details can be found here:
| Oblique shocks and expansion waves | (Prandtl-Meyer expansion waves) |
Update gas data if needed. The default values for air are \(\gamma=1.4\), \(R=287\) \(\mathrm{J/(kg\ K})\), and \(C_p=1005\) \(\mathrm{J/(kg\ K})\) and for the combustion gas \(\gamma=1.333\), \(R=287\) \(\mathrm{J/(kg\ K})\), and \(C_p=1148\) \(\mathrm{J/(kg\ K})\).
| Ratio of specific heats (air) \(\left(\gamma_{air}=C_{p,air}/C_{v,air}\right)\) | ||||||
| Gas constant (air) \(\left(R\right)\) | ||||||
| Specific heat (air) \(\left(C_{p,air}\right)\) |
| Ratio of specific heats (gas) \(\left(\gamma_{gas}=C_{p,gas}/C_{v,gas}\right)\) | ||||||
| Gas constant (gas) \(\left(R\right)\) | ||||||
| Specific heat (gas) \(\left(C_{p,gas}\right)\) |
Description of what the calculator does goes here ...
| Flight Mach number \(\left(M_\infty\right)\) | ||||||
| Altitude | ||||||
| Variation to ISA \(\left(\Delta \mathrm{ISA}\right)\) |
| Turbine entry temperature \(\left(\mathrm{TET}\right)\) | ||||||
| Bypass ratio \(\left(\mathrm{BPR}\right)\) | ||||||
| Intake isentropic efficiency \(\left(\eta_{in}\right)\) | ||||||
| Fan pressure ratio \(\left(\mathrm{FPR} \right)\) | ||||||
| Fan isentropic efficiency \(\left(\eta_{i,fan}\right)\) | ||||||
| LP Compressor pressure ratio \(\left(\mathrm{\Pi_{LPC}} \right)\) | ||||||
| LP Compressor isentropic efficiency \(\left(\eta_{i,LPC}\right)\) | ||||||
| HP Compressor pressure ratio \(\left(\mathrm{\Pi_{HPC}} \right)\) | ||||||
| HP Compressor isentropic efficiency \(\left(\eta_{i,HPC}\right)\) | ||||||
| Combustion efficiency \(\left(\eta_{b}\right)\) | ||||||
| Combustion pressure loss \(\left(1-P_4/P_3\right)\) | ||||||
| HP Turbine isentropic efficiency \(\left(\eta_{i,HPT}\right)\) | ||||||
| LP Turbine isentropic efficiency \(\left(\eta_{i,LPT}\right)\) | ||||||
| Mechanical efficiency \(\left(\eta_{m}\right)\) | ||||||
| Cold nozzle isentropic efficiency \(\left(\eta_{n,cold}\right)\) | ||||||
| Hot nozzle isentropic efficiency \(\left(\eta_{n,hot}\right)\) | ||||||
| Lower heating value \(\left(\mathrm{LHV}\right)\) | ||||||
| Cooling relative flow \(\left(\mathrm{bpr}_c\right)\) |
An expansion region or expansion fan is generated in a supersonic flow when the flow direction needs to change such that the flow area increases - the flow turns out from itself. The expansion region constitutes a collection of an infinite number of Mach waves. Each Mach wave contributes with an infinitesimal change in flow direction and flow properties without introduction of losses i.e., the process is isentropic. Thus, the integrated effect over the expansion region is also isentropic. In the figure below, the sharp expansion corner (left figure) will lead to the generation of a centered simple wave or expansion fan and the gradual expansion (right figure) will generate a simple wave (that might be centered depending on the shape of the wall)

The expansion fan (Prandtl-Meyer expansion) generated at the expansion corner in the figure below will gradually change the flow direction and the end result is a net turning of the flow such that it follows the wall downstream of the corner.

The left and right ends of the expansion fan are defined by the angle of Mach waves in the upstream and downstream region, respectively.

The net turning may be calculated as follows:
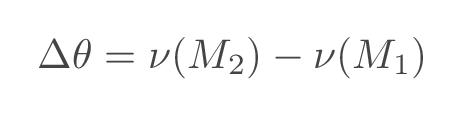
where \(\nu(M)\) is the Prandtl-Meyer function evaluated at a position with Mach number \(M\)
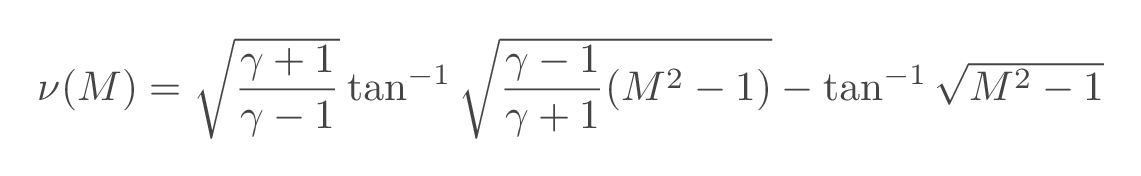
| flow property | change over expansion region |
|---|---|
| density | decreases |
| pressure | decreases |
| temperature | decreases |
| velocity | increases |
| Mach number | increases |
More details can be found here:
| Oblique shocks and expansion waves | (Prandtl-Meyer expansion waves) |
Update gas data if needed. The default values for air are \(\gamma=1.4\), \(R=287\) \(\mathrm{J/(kg\ K})\), and \(C_p=1005\) \(\mathrm{J/(kg\ K})\) and for the combustion gas \(\gamma=1.333\), \(R=287\) \(\mathrm{J/(kg\ K})\), and \(C_p=1148\) \(\mathrm{J/(kg\ K})\).
| Ratio of specific heats (air) \(\left(\gamma_{air}=C_{p,air}/C_{v,air}\right)\) | ||||||
| Gas constant (air) \(\left(R\right)\) | ||||||
| Specific heat (air) \(\left(C_{p,air}\right)\) |
| Ratio of specific heats (gas) \(\left(\gamma_{gas}=C_{p,gas}/C_{v,gas}\right)\) | ||||||
| Gas constant (gas) \(\left(R\right)\) | ||||||
| Specific heat (gas) \(\left(C_{p,gas}\right)\) |
Description of what the calculator does goes here ...
| Select problem type | ||||||
| Mach number \(\left(M\right)\) | ||||||
| temperature ratio (subsonic) \(\left(T/T^*\right)\) | ||||||
| temperature ratio (supersonic) \(\left(T/T^*\right)\) | ||||||
| pressure ratio \(\left(p/p^*\right)\) | ||||||
